Kekongruenan Bangun Datar

Kekongruenan Bangun Datar - Dua bangun atau lebih dikatakan kongruen jika bangun-bangun tersebut memiliki bentuk dan ukuran yang sama serta sudut-sudut yang bersesuaian sama besar.

Kekongruenan Bangun Datar

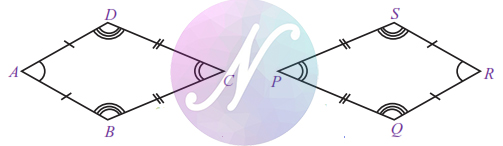
Perhatikan Gambar berikut!

Panjang sisi-sisi yang bersesuaian pada kedua layang-layang tersebut sama besar, yaitu AB = QR = AD = RS dan BC = PQ = CD = SP. Sudut-sudut yang bersesuaian pada kedua laying-layang tersebut juga sama besar, yaitu ∠A = ∠R, ∠C = ∠P, ∠B = ∠Q, dan ∠D = ∠S. Oleh karena itu, layang-layang ABCD dan layang-layang PQRS kongruen, ditulis layang-layang ABCD ≅ layang-layang PQRS.

Contoh Soal Kekongruenan Bangun Datar

Untuk lebih memahami tentang materi Kekongruenan Bangun Datar khusus kelas 9 perhatikan 2 contoh soal berikut ini!

1. Perhatikan gambar berikut!

Tunjukkan bahwa kedua bangun tersebut kongruen.

Jawab:

Panjang sisi-sisi yang bersesuaian pada trapesium ABCD dan trapesium PQRS sama besar, yaitu

AB = PQ,

BC = QR,

CD = RS,   dan

AD = PS.

Sudut-sudut yang bersesuaian pada kedua trapesium tersebut sama besar, yaitu

∠A = ∠P = ∠E = ∠Q   dan

∠C = ∠R = ∠D = ∠S.

Dari jawaban a dan b terbukti bahwa trapesium ABCD ≅ trapesium PQRS.

2. Perhatikan dua bangun datar yang kongruen berikut!

Tentukan besar ∠E.

Jawab :

Oleh karena kedua bangun datar tersebut kongruen, sudut-sudut yang bersesuaian sudah pasti sama besar.

∠A = ∠F = 45°

∠C = ∠H = 60°

∠D = ∠G = 120°

∠B = ∠E = ......?

Jumlah sudut pada bangun datar ABCD = jumlah sudut pada bangun datar EFGH = 360°.

∠E = 360° - (–F + –G + –H )

      = 360° - (45° +120° + 60° )

      = 360° - 225° = 35°

Jadi, ∠E = 35°