Macam-macam Pola Bilangan Kelas 8

Macam-macam Pola Bilangan Kelas 8 - Pada zaman modern saat ini kita dapat menemukan berbagai kejadian atau fakta-fakta yang menggunakan bilangan-bilangan atau angka dengan aturan tertentu, misalnya nomor rumah sebelah kiri jalan dengan nomor ganjil dan sisi kanan dengan nomor genap berderet di pinggir jalan besar atau perumahan. Begitu pula dalam bidang ilmu terapan lain pengunaan bilangan dengan berbagai variasi dan bentuk perhitungannya. Agar kita dapat mengembangkan penemuan-penemuan yang telah ada, maka kita perlu mengenal dan memahami latar belakang dari alat ataupun ilmu-ilmu yang ada, diantaranya barisan bilangan dengan berbagai kaitannya.

Macam-macam Pola Bilangan Kelas 8

Pola Bilangan adalah sebuah barisan bilangan yang membentuk pola tertentu sehingga dapat diperoleh rumus umum untuk menentukan suku ke – n dari suatu pola bilangan.

Ada beberapa pola bilangan yang sering dipakai yaitu :

1. Pola Bilangan Ganjil

Pola bilangan ganjil adalah barisan loncat yang terdiri atas kumpulan bilangan ganjil. Barisan bilangan yang merupakan pola bilangan ganjil adalah 1, 3, 5, 7, dan seterusnya. Rumus U_n untuk pola bilangan ganjil dan bentuk pola bilangan ganjil dapat dilihat seperti berikut :

Perhatikan bahwa pola suku – sukunya :

U₁ = 1 = 2. 1 – 1

U₂ = 3 = 2. 2 – 1

U₃ = 5 = 2.3 – 1

U₄ = 7 = 2.4 – 1

⋮

U_n = 2.n – 1

Dengan memperhatikan urutan suku-sukunya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan tertentu, sehingga diperoleh rumus suku ke–n adalah U_n = 2n – 1.

2. Pola Bilangan Genap

Hampir sama seperti pola bilangan ganjil, pada pola bilangan genap juga merupakan barisan bilangan loncat yang merupakan kumpulan bilangan genap. Contoh pola bilangan genap: 2, 4, 6, 8, dan seterusnya. Rumus U_n pola bilangan genap dan bentuk pola bilangan genap diberikan seperti berikut.

Perhatikan bahwa pola suku – sukunya :

U₁ = 2 = 2. 1

U₂ = 4 = 2. 2

U₃ = 6 = 2. 3

U₄ = 8 = ...

U₅ = 10 = ...

⋮

U_n = ...

Dengan memperhatikan urutan suku – sukunya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan tertentu, sehingga diperoleh rumus suku ke–n adalah U_n = 2n

3. Pola Bilangan Segitiga

Pada pola bilangan segitiga, barisan bilangan yang mewakili bundaran yang dapat membentuk segitiga. Contoh pola bilangan segitiga: 1, 3, 6, 10, dan seterusnya. Rumus U_n pola bilangan segitiga dan bentuk pola bilangan segitiga diberikan seperti gambar di bawah

Perhatikan bahwa pola suku – sukunya :

U₁ = 1 = 1/2. 1 . (1 + 1)

U₂ = 3 = 1/2. 2 . (2 + 1)

U₃ = 6 = 1/2. 3 . (3 + 1)

U₄ = 10 = ...

U₅ = ... = ...

U₆ = ... = ...

⋮

U_n = ...

Dengan memperhatikan urutan suku - sukunya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan tertentu, sehingga diperoleh rumus suku ke–n adalah U_n = Un = ½ n(n+1).

4. Pola Bilangan Persegi

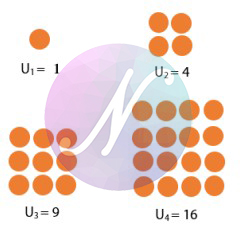
Untuk pola bilangan persegi memiliki pola yang sama dengan pola bilangan pangkat dua. Barisan bilangan yang menyusun pola bilangan persegi juga merupakan pola bilangan pangkat dua. Sehingga rumus U_n pola bilangan persegi dapat dinyatakan sebagai pangkat dua dari suatu bilangan. Contoh pola bilangan persegi: 2, 4, 9, 16, dan seterusnya.

Perhatikan bahwa pola suku – sukunya :

U₁ = 2 = 1²

U₂ = 4 = 2²

U₃ = 9 = 3²

U₄ = 16 = ...

U₅ = ... = ...

U₆ = ... = ...

⋮

U_n = ...

Dengan memperhatikan urutan suku - sukunya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan tertentu, sehingga diperoleh rumus suku ke–n adalah U_n = n².

5. Pola Bilangan Persegi Panjang

Contoh pola bilangan persegi panjang: 2, 6, 12, 20, dan seterusnya. Rumus U_n untuk pola bilangan persegi dapat dilihat dari bentuk pola bilangan seperti pada gambar berikut.

Perhatikan bahwa pola suku – sukunya :

U₁ = 2 = 1 . (1 + 1)

U₂ = 6 = 2 . (2 + 1)

U₃ = 12 = 3 . (3 + 1)

U₄ = 20 = ....

U₅ = ... = ....

U₆ = ... = ....

⋮

U_n = ....

Dengan memperhatikan urutan suku-sukunya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan, sehingga diperoleh rumus suku ke–n adalah U_n = Un = n(n+1).

6. Pola Bilangan Segitiga Pascal

Pola bilangan segitiga pascal merupakan jumlah bilangan – bilangan dari setiap baris pada segitiga pascal. Contoh pada baris ke 4 dari segitiga pascal terdiri atas barisan bilangan 1, 2, dan 1 sehingga bilangan U₄ sama dengan 1 + 2 + 1 = 4. Barisan bilangan segitiga pascal adalah 1, 2, 4, 8, 16, 32, dan seterusnya.

Bentuk pola bilangan segitiga pascal dapat dilihat pada gambar berikut :

Perhatikan bahwa pola suku – sukunya :

U₁ = 1 = 2^1-1

U₂ = 2 = 2^2-1

U₃ = 4 = 2^3-1

U₄ = 8 = ....

U₅ = 16 = ....

U₆ = 32 = ....

⋮

U_n = ....

Dengan memperhatikan urutan suku - sukunya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan, sehingga diperoleh rumus suku ke – n adalah U_n = Un = 2^n-1.

7. Pola bilangan Fibonacci

Pola bilangan Fibonacci adalah pola bilangan rekursif (pemanggilan ulang/pengulangan) yang ditemukan oleh seorang matematikawan berkebangsaan Italia yang bernama Leonardo da Pisa. Pola bilangan Fibonacci diperoleh dari menjumlah dua bilangan sebelumnya. Contoh barisan bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, dan seterusnya.

Perhatikan bahwa pola suku – sukunya :

U₁ = 1 = 1

U₂ = 1 = 1

U₃ = 2 = 1 + 1 = U₁ + U₂

U₄ = 3 = 1 + 2 = U₂ + U₃

U₅ = 5 = 2 + 3 = U₃ + U₄

U₆ = 8 = .... + .... = U... + U...

U₇ = 13 = .... + .... = U... + U...

⋮

U_n = U...... + U.......

Dengan memperhatikan urutan bilangannya maka akan tampak bahwa pola bilangan tersebut mengikuti suatu aturan, sehingga diperoleh rumus suku ke – n adalah U_n = U_n-1 + U_1-2.