Soal Transformasi SMP Kelas 9 dan Pembahasannya - Kali ini kita akan membahas beberapa butir soal transformasi kelas 9 dilengkapi dengan kunci serta pembahasannya. Transformasi geometri untuk tingkatan SMP kelas 9 dibagi menjadi 4 bagian, mulai dari pencerminan (refleksi), pergeseran (translasi), perputaran (rotasi) dan dilatasi.
Soal Transformasi SMP Kelas 9 dan Pembahasannya
Soal Pencerminan (Refleksi)
1. Titik P (2, 1) dicerminkan terhadap sumbu Y, maka P' adalah...
a. (1, 2)
b. (-1, -2)
c. (-2, 1)
d. (2, 1)
Pembahasan :
Rumus : A (x,y) direfleksikan terhadap sumbu Y hasilnya A' (-x,y)
Jadi P (2,1) direfleksikan terhadap sumbu Y hasilnya P' (-2,1)
Jawaban yang benar adalah C.
2. Titik B (3, 2) dicerminkan terhadap sumbu X, maka B' adalah...
a. (2, 3)
b. (-3, -2)
c. (-3, 2)
d. (3, -2)
Pembahasan :
Rumus : A (x,y) direfleksikan terhadap sumbu X hasilnya A' (x,-y)
Jadi B (3,2) direfleksikan terhadap sumbu X hasilnya B' (3,-2)
Jawaban yang benar adalah D
3. Titik (-4, 2) direfleksikan terhadap garis y = -x. Koordinat titik bayangannya adalah...
a. (2, -4)
b. (-2, 4)
c. (2, 4)
d. (4, -2)
Pembahasan :
Rumus : A (x,y) direfleksikan terhadap garis y = -x hasilnya A' (-y,-x)
Jadi titik (-4,2) direfleksikan terhadap garis y = -x hasilnya (-2,4)
Jawaban yang benar adalah B
4. Jika titik Q (7, 5) dicerminkan terhadap garis x = 3 maka koordinat titik bayangannya adalah..
a. (5, -1)
b. (5, 1)
c. (-1, 5)
d. (-1, -5)
Pembahasan :
Rumus : A (x,y) direfleksikan terhadap garis x = m hasilnya A' ((2(m)-x), y)
Jadi titik Q (7,5) direfleksikan terhadap garis x = 3 hasilnya Q' (-1, 5)
Jawaban yang benar adalah C
5. Bayangan titik P(-4, 5) oleh refleksi terhadap garis y = -x dilanjutkan dengan refleksi terhadap garis x = 2 adalah...
a. P’(-5, 4)
b. P’ (4, -5)
c. P’ (9, 4)
d. P, (-4, 9)
Pembahsan :
Soal ini kita hanya perlu melakukan dua kali refleksi
Refleksi I garis y = -x
Rumus : A (x,y) direfleksikan terhadap garis y = -x hasilnya A' (-y,-x)
Jadi P (-4,5) direfleksikan terhadap garis y = -x hasilnya P' (-5,4)
Refleksi II garis x = 2
Rumus : A (x,y) direfleksikan terhadap garis x = m hasilnya A' ((2(m)-x), y)
Jadi titik P' (-5,4) direfleksikan terhadap garis x = 2 hasilnya P'' (9, 4)
Jawaban yang benar C
6. Bayangan dari titik A(-3, 2) yang direfleksikan terhadap garis x = -2 dilanjutkan terhadap garis y = 3 adalah...
a. A'(-1, 4)
b. A'(4, -1)
c. A'(1, -4)
d. A'(-4, 1)
Pembahasan :
Soal ini kita hanya perlu melakukan dua kali refleksi
Refleksi I garis x = -2
Rumus : A (x,y) direfleksikan terhadap garis x = m hasilnya A' ((2(m)-x), y)
Jadi A (-3,2) direfleksikan terhadap garis x = -2 hasilnya A' (-1, 2)
Refleksi II garis y = 3
Rumus : A (x,y) direfleksikan terhadap garis y = 3 hasilnya A' (x, (2(n) - y)
Jadi A' (-1,2) direfleksikan terhadap garis y = 3 hasilnya A'' (-1, 4)
Jawaban yang benar A
7. Koordinat titik K (2,-4) dicerminkan terhadap garis y = x, maka koordinat dari bayangan yang terbentuk adalah...
a. (-4, -2)
b. (4, -2)
c. (-2, 4)
d. (-4, 2)
Pembahasan :
Rumus : A (x,y) direfleksikan terhadap garis y = x hasilnya A' (y,x)
Jadi K (2,-4) direfleksikan terhadap garis y = x hasilnya K' (-4,2)
Jawaban yang benar D
8. Jika garis x - 2y = 3 dicerminkan terhadap sumbu Y, maka persamaan bayangannya adalah ...
a. -x - 2y = 3
b. x + 2y = 3
c. -x - 2y = -3
d. -x + 2y = -3
Pembahasan :
Rumus : A (x,y) direfleksikan terhadap sumbu Y hasilnya A' (-x,y)
Jadi nilai x berganti menjadi -x jadi persamaan garis berubah menjadi -x - 2y = 3
Jawaban yang benar A
Soal Pergeseran (Translasi)
1. Titik A (7, -6) ditranslasikan oleh T = (-2, 4), maka koordinat titik A’ adalah...
a. (9, -10)
b. (-5, -2)
c. (5, -2)
d. (-9, 10)
Pembahasan :
Rumus : A (x,y) ditanslasikan terhadap titik (a,b) hasilnya A' ((x + a), (y + b))
Jadi A (7,-6) ditanslasikan terhadap titik (-2,4) hasilnya A' (5, -2)
Jawababn yang benar C
2. Jika titik (2, -1) ditranslasikan oleh T = (3, 2) maka bayangannya adalah...
a. (5, 1)
b. (2, 1)
c. (1, 2)
d. (-5, -1)
Pembahasan :
Rumus : A (x,y) ditanslasikan terhadap titik (a,b) hasilnya A' ((x + a), (y + b))
Jadi (2,-1) ditanslasikan terhadap titik (3,2) hasilnya (5, 1)
Jawaban yang benar A
3. Jika titik G'(4, -1) adalah bayangan titik dari G (7, -5) oleh translasi T, maka nilai T adalah ...
a. (2, 5)
b. (-3, 4)
c. (1, 7)
d. (4, 2)
Pembahasan :
Soal ini meminta kita untuk mencari nilai koordinat translasi yaitu nilai a dan nilai b
x + a = 4 (nilai 4 diambil dari hasil translasi koordinat x; G'(4, -1) )
7 + a = 4 (nilai 7 diambil dari koordinat awal x; G'(4, -1) )
a = 4 - 7
a = -3
y + b = -1 (nilai -1 diambil dari hasil translasi koordinta y ; G (7, -5) )
-5 + b = -1 (nilai -5 diambil dari koordinat awal y ; G (7, -5) )
b = -1 + 5
b = 4
Jadi T (a,b) = T (-3,4)
Jawaban yang benar B
4. Koordinat bayangan titik A(-3, 4) oleh translasi T = (3, 6) adalah...
a. A'(0, 10)
b. A'(10, 0)
c. A'(-10, 0)
d. A'(0, -10)
Pembahasan :
Rumus : A (x,y) ditanslasikan terhadap titik (a,b) hasilnya A' ((x + a), (y + b))
Jadi A (-3,4) ditanslasikan terhadap titik (3,6) hasilnya A' (0, 10)
Jawaban yang benar A
5. Koordinat bayangan titik A(5, -2) pada translasi (5, -3) adalah..
a. A'(2, -1)
b. A'(2, 0)
c. A'(7, -3)
d. A'(10, -5)
Pembahasan :
Rumus : A (x,y) ditanslasikan terhadap titik (a,b) hasilnya A' ((x + a), (y + b))
Jadi A (5,-2) ditanslasikan terhadap titik (5,-3) hasilnya A' (10, -5)
Jawaban yang benar D
6. Jika garis 3x – 2y = 6 ditranslasikan oleh T = (3, -4) maka bayangan garis tersebut adalah...
a. 3x – 2y = 6
b. 3x – 2y = 3
c. 3x – 2y = -11
d. 3x – 2y = 23
Pembahasan :
x' = (x + 3)
y' = (y – 4)
3x' – 2y' = 6
3(x + 3) – 2 (y – 4) = 6
3x + 9 – 2y + 8 = 6
3x – 2y + 17 = 6
3x – 2y = 6 – 17
3x - 2y = -11
Jawaban yang benar C.
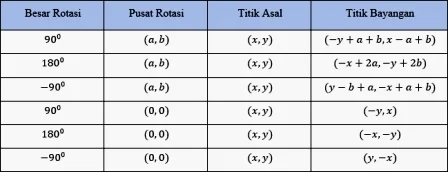
Soal Perputaran (Rotasi)
1. Titik P (8, 5) dirotasikan sejauh 900 terhadap titik pusat O (0, 0) berlawanan arah jarum jam. Nilai P' adalah...
a. (5, 8)
b. (-8, 5)
c. (-8, -5)
d. (-5, 8)
Pembahasan :
Rumus : A (x,y) dirotasi sebesar 900 pusat rotasi (0,0) dan titik asal (x,y) hasilnya A' (-y, x)
Jadi P (8,5) dirotasi 900 pusat rotasi (0,0) hasilnya P' (-5, 8)
Jawaban yang bendar D
2. Bayangan dari titik A(-2, 3) yang dirotasikan sebesar 900 berlawanan arah jarum jam adalah...
a. A'(2, -3)
b. A'(3, -2)
c. A'(-3, -2)
d. A'(3, 2)
Pembahasan :
Rumus : A (x,y) dirotasi sebesar 900 pusat rotasi (a,b) dan titik asal (x,y) hasilnya A' (-y, x)
Jadi A (-2,3) dirotasi 900 pusat rotasi (0,0) hasilnya A' (-3, -2)
Jawaban yang benar C
3. Persamaan bayngan garis 3x – y + 2 = 0 yang dicerminkan terhadap garis y = x kemudian dilanjutkan dengan rotasi 900 terhadap titik asal adalah...
a. 3x + y + 2 = 0
b. 3x – y – 2 = 0
c. 3y – x + 2 = 0
d. x – 3y – 2 = 0
Pembahasan :
Soal ini meminta kita melakukan dua langkah transformasi, pertama pencerminan kemudian hasil pencerminan dirotasi.
Pencerminan (refleksi) terhadap garis y = x
Rumus : A (x,y) direfleksikan terhadap garis y = x hasilnya A' (y,x)
x' = y
y' = x
3x' – y' + 2 = 0
3y – x + 2 = 0
Perputaran (rotasi) 900 terhadap titik asal
Rumus : A (x,y) dirotasi sebesar 900 pusat rotasi (0,0) dan titik asal (x,y) hasilnya A' (-y, x)
x' = -y
y' = x
3y' – x' + 2 = 0
3(x) – (-y) + 2 = 0
3x + y + 2 = 0
Jawaban yang benar A
4. Titik A (-3, 6) dirotasikan dengan pusat di O(0, 0) sebesar 1800, maka bayangan koordinat titik A adalah..
a. (9-3, -6)
b. (3, -6)
c. (-6, -3)
d. (-6, 3)
Pembahasan :
Rumus : A (x,y) dirotasi sebesar 1800 pusat rotasi (0,0) dan titik asal (x,y) hasilnya A' (-x, -y)
Jadi A (-3,6) dirotasi 1800 pusat rotasi (0,0) hasilnya A' (3, -6)
Jawaban yang benar B
Soal Dilatasi
1. Koordinat bayangan titik C (9, -6) didilatasi terhadap titik pusat O dengan faktor skala – 1/3 adalah ...
a. (-2, 3)
b. (2, 3)
c. (3, 2)
d. (-3, 2)
Pembahasan :
Rumus : A (x,y) didilatasi dengan pusat (0,0) faktor skala k titik asal (x,y) hasilnya A' (kx, ky)
Jadi C (9,-6) didilatasi dengan pusat (0,0) faktor skala -1/3 hasilnya C' (-3, 2)
Jawaban yang benar D
2. Titik Q (3, -6) didilatasi terhadap titik pusat M (-2, 3) dengan faktor skala 2, maka bayangan titik Q adalah...
a. (7, 10)
b. (8, -15)
c. (-3, -7)
d. (-6, 8)
Pembahasan :
Rumus : A (x,y) didilatasi dengan pusat (a,b) faktor skala k titik asal (x,y) hasilnya A' (k(x - a) + a, k(y - b) + b)
Jadi Q (3,-6) didilatasi dengan pusat M (-2,3) faktor skala 2 hasilnya Q' (8,-15)
Nilai 8 diambil dari
x' = k (x - a) + a dimana k = 2, x = 3, dan a = -2
x' = 2 (3 - (-2)) + -2 = 10 - 2 = 8
Nilai -15 diambil dari
y' = k (y - b) + b dimana k =2, y = -6, dan b = 3
y' = 2 (-6 - 3) + 3 = -18 + 3 = -15
Jawaban yang benar B
3. Bayangan titik P (-2, 3) oleh dilatasi [O, k] adalah P’(4, -6), sehingga bayangan titik Q (3, -2) oleh dilatasi [O, 4k] adalah...
a. (-24, 16)
b. (24, -16)
c. (-24, -16)
d. (24, 16)
Pembahasan :
Soal ini agak berbeda dengan soal-soal sebelumnya, di sini kita terlebih dulu harus memahami maksud dari soal. Biasanya soal seperti ini kita akan bingun karena kita tidak melihat dengan jelas faktor skala dan pusat dilatasi. Padahal sebenarnya faktor skala dan pusat dilatasi ada hanya dituliskan dalam bentuk lain yaitu [0,k]. Berarti soal ini faktor skalanya adalah k dan pusat dilatasi (0,0)
Untuk menyelesaikan soal ini terlebih dahulu kita mencari faktor skalanya
Rumus : Rumus : A (x,y) didilatasi dengan pusat (0,0) faktor skala k titik asal (x,y) hasilnya A' (kx, ky)
Dari data P (-2,3) dan P' (4,-6) serta [0,k] kita bisamenentukan besar nilai k
Jadi x' = kx dan y' = ky dan nilai x' = 4, y' = -6, x = -2, dan y = 3, sehingga
4 = k . -2
k = 4/-2
k = -2
Sekarang kita bisa mencari Q (3, -2) oleh dilatasi [O, 4k] karena kita sudah memiliki nilai k = -2
Faktor skala untuk dilatasi Q adalah 4k, berarti nilai faktor skala untuk Q adalah k = -8
Rumus : Rumus : A (x,y) didilatasi dengan pusat (0,0) faktor skala k titik asal (x,y) hasilnya A' (kx, ky)
Jadi Q (3,-2) didilatasi dengan pusat (0,0) faktor skala -8 hasilnya Q' (-24,16)
Jawaban yang benar adalah A
4. Diketahu titik P (12, -5) dan A (-2, 1). Bayangan titik P oleh dilatasi [A, ½ ] adalah...
a. P' (-2, 5)
b. P' (2, 5)
c. P' (5, -2)
d. P' (-5, -2)
Pembahasan :
Rumus : A (x,y) didilatasi dengan pusat (a,b) faktor skala k titik asal (x,y) hasilnya A' (k(x - a) + a, k(y - b) + b)
x ' = 1/2 (12 - (-2)) + (-2) = 5
y' = 1/2 (-5 - 1) + 1 = 2
Jadi P (12,-5) didilatasi dengan pusat (-2,1) faktor skala 1/2 hasilnya Q' (5,-2)