Pencerminan (Refleksi) khusus Kelas 9 Beserta Contohnya - Kali ini kita akan membahas masalah pencerminan (refleksi) khusus untuk siswa kelas 9. Agar lebih mudah memahami admin memberikan gambar beserta contohnya untuk tiap penjelasan pencerminan. Di dalam materi ada 7 pembahasan singkat mengenai refleksi, mulai dari refleksi terhadap sumbu -x, sumbu y, titik asal (0,0), garis x = y, garis y = - x, garis y = k dan garis x = h.
Pencerminan (Refleksi) khusus Kelas 9 Beserta Contohnya
Refleksi atau pencerminan merupakan satu jenis transformasi yang memindahkan setiap titik pada suatu bidang dengan mengggunakan sifat bayangan cermin dari titik-titik yang dipindahkan. Jika belum memahami transformasi anda bisa melihat penjelasannya di Pengertian Transformasi dalam Matematika.
Perhatikan gambar di bawah.
Gambar di atas menunjukkan contoh refleksi (pencerminan) bangun datar ABCDE pada garis m. Perhatikan bahwa ruas garis yang menghubungkan titik dan bayangannya tegak lurus terhadap garis m. Garis m disebut garis refleksi untuk ABCDE dan bayangannya A’B’C’D’E’.
Karena E terletak pada garis refleksi, titik awal dan bayangannya berada di titik yang sama. Jarak antara A terhadap garis m sama dengan jarak A’ terhadap garis m, begitu pula untuk titik sudut yang lainnya dan bayangannya yang memiliki jarak sama terhadap garis refleksi m.
Jika diketahui sebarang titik dengan koordinat (x, y) pada koordinat kartesius, maka koordinat bayangan hasil pencerminannya dapat dilihat pada Tabel 1 berikut ini.
Pencerminan Terhadap Sumbu-x
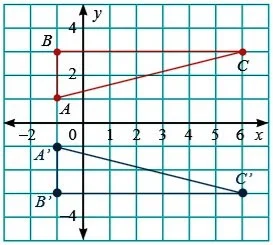
Segitiga ABC berkoordinat di A (–1, 1), B (–1, 3), dan C (6, 3). Gambar segitiga ABC dan bayangannya yang direfleksikan terhadap sumbu-x. Bandingkan koordinat titik-titik ABC dengan koordinat bayangannya.
Penyelesaian:
Perhatikan bahwa titik A berada 1 satuan di atas sumbu-x, maka bayangannya adalah A’ yang terletak 1 satuan di bawah sumbu-x. Sedangkan titik B dan C berada pada 3 satuan di atas sumbu-x, maka banyangannya adalah B’ dan C’ yang terletak 3 satuan di bawah sumbu-x. Dengan demikian diperoleh koordinat masing-masing titik dan bayangannya adalah sebagai berikut:
A (–1, 1) → A’ (–1, –1)
B (–1, 3) → B’ (–1, –3)
C (6, 3) → C’ (6, –3)
Hubungkan ketiga titik sehingga membentuk segitiga A’B’C’.
Pencerminan Terhadap Sumbu -y
Pada dasarnya, pencerminan terhadap sumbu y merupakan mengubah posisi objek pada koordinat kartesius dengan cara mencerminkan objek tersebut terhadap sumbu y. Untuk lebih jelasnya, ilustrasi berikut. Misalkan titik (x,y) dicerminkan terhadap sumbu y. Maka, didapatkan bayangan (-x,y) sebagai hasil pencerminannya seperti pada gambar di bawah.
Sehingga, dapat disimpulkan jika titik (x,y) dicerminkan terhadap sumbu y, maka diperoleh koordinat bayangan (x′,y′) = (-x,y)
Pencerminan Terhadap Titik Asal O(0,0)
Untuk pencerminan terhadapa titik asal cukup menarik karena satu-satunya pencerminan yang mengacu hanya pada satu titik, yaitu titik (0,0). Jika sebuah titik koordinat (a, b) direfleksikan pada titik asal akan diperoleh bayangan pada titik (-a, -b). Seperti diperlihatkan pada gambar berikut.
Jadi hasil pencerminan titik asal akan selalu menghasilkan (-x, -y), misalnya koordinat A (4,2) direfleksikan terhadapa titik asal akan diperoleh bayanan A' (-4,-2).
Pencerminan Terhadap Garis y = x
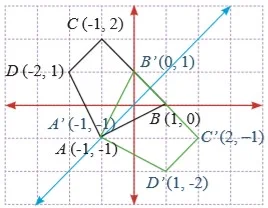
Diketahui segi empat ABCD yang memiliki koordinat di A (-1, -1), B (1, 0), C (-1, 2) dan D (-2, 1) direfleksikan terhadap garis y = x. Gambar ABCD dan bayangannya yang direfleksikan terhadap garis y = x. Bandingkan koordinat titik-titik ABCD dengan koordinat bayangannya.
Penyelesaian:
Untuk menentukan bayangan titik-titik segi empat ABCD, perhatikan jarak titik B ke garis y = x. Dari titik B buat garis yang tegak lurus ke garis y = x (disebut garis BB’) kemudian dapatkan titik B’ yang memiliki jarak yang sama besar dengan jarak titik B ke garis y = x. Titik B’merupakan bayangan titik B hasil refleksi terhadap garis y = x. Dengan demikian diperoleh koordinat B’ (0, 1). Gunakan cara yang sama, sehingga diperoleh koordinat bayangan untuk titik-titik yang lainnya sebagai berikut:
A (–1, –1) → A’ (–1, –1)
B (1, 0) → B’ (0, 1)
C (–1, 2) → C’ (2, –1)
D (–2, 1) → D’ (1, –2)
Hubungkan keempat titik sehingga membentuk segi empat A’B’C’D’.
Pencerminan Terhadap Garis y = -x
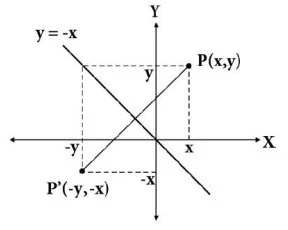
Hasil pencerminan terhadap garis y = -x akan menghasilkan bayangan (-y, -x), agar lebih cepat paham perhatikan gambar berikut ini.
Jadi jika sebuah titik koordinat P (1,2) direfleksikan terhadapa garis y = -x akan dihasilkan bayangan P' (-2, -1).
Pencerminan Terhadap Garis y = k
Untuk pencerminan terhadap garis y = h kita bisa memahami dengan baik jika kita mampu membuat garis cermin y = k. Di mana nilai h merupakan bilangan asli bisa 1, 2, 3, ... atau -1, -2, -3 dan seterusnya. Untuk lebih jelasnya perhatikan gambar berikut.
Misalnya titik A (2, 1) direfleksikan terhadap garis y = 2, maka akan dihasilkan bayangan pada titik A' (2, 3). Nilai 3 diperoleh dari 2k - b, di mana nilai k = 2 dan b = 1 sehingga 2 x 2 - 1 = 3.
Pencerminan Terhadap Garis x = h
Penceminan terhadap garis x = h sebenarnya tidak jauh berbeda dengan pencerminan terhadap sumbu -x. Hanya saja pada pencerminan garis x = h, nilai tidak sama dengan nol. Untuk lebih jelasnya perhatikan gambar berikut.
Pada gambar di atas cermin berada pada x = 2, berarti nilai h = 2. Koordinta titik A (3,5) direfleksikan terhadap garis x = 2 diperoleh bayangan A' (1,5). Dari mana diperoleh A' (1,5)? diperoleh dari rumus pencerminan garis x = h,yaitu ( 2h - x, y) berarti ( 2 x 2 - 3, 5) = ( 1,5).
Jadi untuk menguasai refleksi anda harus bisa menggambar garis cermin dan menghafal rumus pencerminan yang ada pada tabel 1. Karena soal pencerminan biasanya menanyakan 2 hal, yaitu gambar hasil pencerminan dan hasil pencerminan. Di mana ketika soal berupa koordinat biasa yang diminta adalah gambar dan koordinat hasil pencerminan, jika soal berupa bangun datar biasanya yang diminta adalah gambar saja untuk tingkatan SMP kelas 9.