Dilatasi Transformasi Matematika Khusus Kelas 9 - Semua transformasi yang telah kita pelajari refleksi, translasi, dan rotasi menghasilkan gambar yang sama dengan gambar aslinya. Dilatasi adalah jenis lain dari transformasi. Namun, bayangan dilatasi mungkin memiliki ukuran yang berbeda dari gambar aslinya. Dilatasi adalah transformasi yang mengubah ukuran sebuah gambar. Dilatasi membutuhkan titik pusat dan faktor skala. Apa itu titik pusat dilatasi dan faktor skala?
Dilatasi Transformasi Matematika Khusus Kelas 9
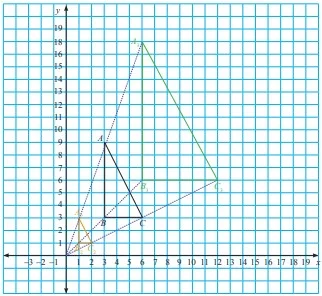
Gambar di bawah ini menunjukkan bagaimana dilatasi dapat menghasilkan bayangan yang lebih besar dan bayangan yang lebih kecil dari aslinya. Segitiga ABC didalatasi dengan pusat dilatasi titik awal P (0, 0) sehingga menghasilkan segitiga A2 B2 C2 dan segitiga A3 B3 C3 .
Berapakah koordinat dari titik A, B, dan C? Berapakah koordinat dari titik A2 , B2 , dan C2 ? Berapakah koordinat dari titik A3 , B3 , dan C3 ? Perhatikan segitiga A2 B2 C2 dan segitiga ABC. Berapakah panjang PA2 jika dibandingkan dengan PA? Bagaimana dengan perbandingan kedua sisi yang lain? Apakah sama? Coba lengkapi bagian kosong di bawah ini untuk memudahkanmu melihat hubungan antara segitiga A2 B2 C2 dan segitiga ABC.
Untuk mengisi nilai faktor skala di atas kita bisa memulai dengan menentukan koordinat tiap titik :
A (3,9), B (3,3), C (6,3)
A2 (1,3), B2 (1,1), C2 (2,1)
A3 (6,18), B3 (6,6), C3 (12,6)
Kalau sudah bisa menentukan tiap titik koordinat, sisa kita melihat perubahan gambar segitiga ABC menjadi segitiga A2 B2 C2 dan segitiga A3 B3 C3.
Segitiga ABC menjadi segitiga A2 B2 C2 mengalami perubahan ukuran dari besar menjadi kecil, agar bisa menjadi kecil harus dikalikan dengan bilangan pecahan. Berapa nilai pecahan tersebut? besarnya adalah 1/3. Perhatikan jika A (3,9), B (3,3), C (6,3) dikalikan dengan faktor skala 1/3 akan menghasilkan A2 (1,3), B2 (1,1), C2 (2,1).
Segitiga ABC menjadi segitiga A3 B3 C3 mengalami perubahan ukuran dari kecilmenjadi besarl, agar bisa menjadi besar harus dikalikan dengan bilangan bukan pecahan. Berapa nilai bilangan tersebut? besarnya adalah 2. Perhatikan jika A (3,9), B (3,3), C (6,3) dikalikan dengan faktor skala 2 akan menghasilkan A3 (6,18), B3 (6,6), C3 (12,6).
Jadi jika ingin mengisi faktor skala di atas cukup menggunakan faktor skala 1/3 saja karena yang ditanyakan adalah faktor skala antara segitiga ABC dengan A2 B2 C2.
Berapakah besarnya faktor skala segitiga A2 B2 C2 yang merupakan hasil dilatasi dari segitiga ABC?
Jawab : 1/3
Dengan cara yang sama, berapakah faktor skala Segitiga A3 B3 C3 yang merupakan hasil dilatasi segitiga ABC?
Jawab : 2
Dilatasi terhadap titik pusat merupakan perkalian dari
koordinat tiap-tiap titik pada suatu bangun datar dengan faktor skala sebesar
k. Faktor skala menentukan apakah suatu dilatasi merupakan pembesaran atau
pengecilan. Secara umum dilatasi dari suatu koordinat (x, y) dengan faktor
skala k akan menghasilkan koordinat (kx, ky) atau dapat ditulis (x, y) → (kx,
ky). Ketika k > 1 maka dilatasi tersebut termasuk ke dalam pembesaran,
tetapi jika 0 < k < 1 maka dilatasi tersebut termasuk ke dalam
pengecilan. Untuk memperbesar atau memperkecil bangun, letak pusat dilatasi
dapat di dalam, di luar, atau pada tepi bangun yang akan didilatasikan.
Untuk memudahkan anda belajar dilatasi transformasi khusus kelas 9, berikut ini tabel rumus dilatasi.
Contoh Soal Dilatasi
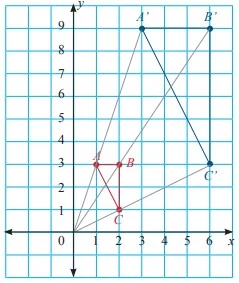
- Diketahui segitiga ABC dengan titik sudut masing-masing A (1, 3), B (2, 3), dan C (2, 1). Gambar segitiga ABC dan bayangannya setelah didilatasi dengan faktor skala 3 dengan pusat dilatasi titik awal.
Penyelesaian:
|
Titik sudut ABC |
(3x, 3y) |
Titik sudut A’B’C’ |
|
A (1, 3) |
(3 × 1, 3 × 3) |
A’ (3, 9) |
|
B (2, 3) |
(3 × 2, 3 × 3) |
B’ (6, 9) |
|
C (2, 1) |
(3 × 2, 3 × 1) |
C’ (6, 3) |
- Persegi panjang KLMN berkoordinat di K (2, 0), L (3, 0), M (3, 2) dan N (2, 2). Tentukan koordinat K’L’M’N’yang merupakan bayangan dari persegi panjang KLMN setelah didilatasi dengan pusat dilatasi di titik P (1, 4) dan faktor skala 2.
Penyelesaian
Langkah 1
Tentukan titik P dan gambar persegi panjang KLMN pada bidang koordinat.
Langkah 2
Buat garis dari titik P sehingga PK’= 2PK
PL’ = 2PL, PM’ = 2PM, dan PN’ = 2PN.
Sehingga diperoleh titik-titik koordinat bayangan K, L, M, dan N adalah sebagai berikut.
K’(3, -4), L (5, –4), M (5, 0), dan N’ (3, 0).
Langkah 3
Hubungkan titik-titik K’, L’, M’, dan N’ sehingga terbentuk persegi panjang K’L’M’N’.
Jadi untuk menyelesaikan soal seputar dilatasi yang perlu anda perhatikan adalah faktor skala, jika faktor skala berupa pecahan maka hasil dilatasi diperkecil. Sebaliknya jika faktor skala bukan pecahan, maka hasil dilatasi diperbesar. Dan jangan lupa perhatikan titik pusat dilatasi! kadang soal menggunakan titik pusat (0,0) atau titik pusat bukan (0,0).